(2/2) ラングランズ・プログラム、谷山・志村・ヴェイユ予想、佐藤・テイト予想
#数学 E.フレンケルさんは数学ミステリー白熱教室第3回で楕円曲線y^2+y=x^3-x^2という「いつものあれ」を題材に色々説明していました。計算のアルゴリズムは明瞭。パソコンなどでテレビと同じ結果を再現したければついでに別の深い事実についても確認した方がよいと思います。続く
#数学 いつもの楕円曲線y^2+y=x^3-x^2の素数位数pの有限体での解の個数の表を作るだけで、ヴェイユ予想のリーマン予想の類似部分、谷山・志村・ヴェイユ予想、佐藤・テイト予想の3つの予想の特別な場合をこの特別な場合に数値的に確認できます。続く
#数学 続き。実際の確認の仕方は https://twitter.com/genkuroki/status/671257536218193920 … 以降の連ツイで詳しく説明しておきました。きれいでわかりやすいグラフが描けたら教えて下さい。グラフの情報を拡散します。続く
#数学 続き。佐藤sin^2予想(=佐藤・テイト予想)を佐藤幹夫さんが発見するために必要になったコンピューターによる計算をやった難波完爾さんによる数学史的に貴重な証言を http://www2.tsuda.ac.jp/suukeiken/math/suugakushi/sympo16/16_8nanba.pdf … で読めます(これは非常におすすめ)。続く
#数学 続き。難波完爾さんは楕円曲線y^2=x(x^2+x+1)とη(x)^2 η(5x)^5を例に色々説明しています。E.フレンケルさんが使った「いつものあれ」以外の例を計算してみたい人はこちらもやってみるとよいと思います。
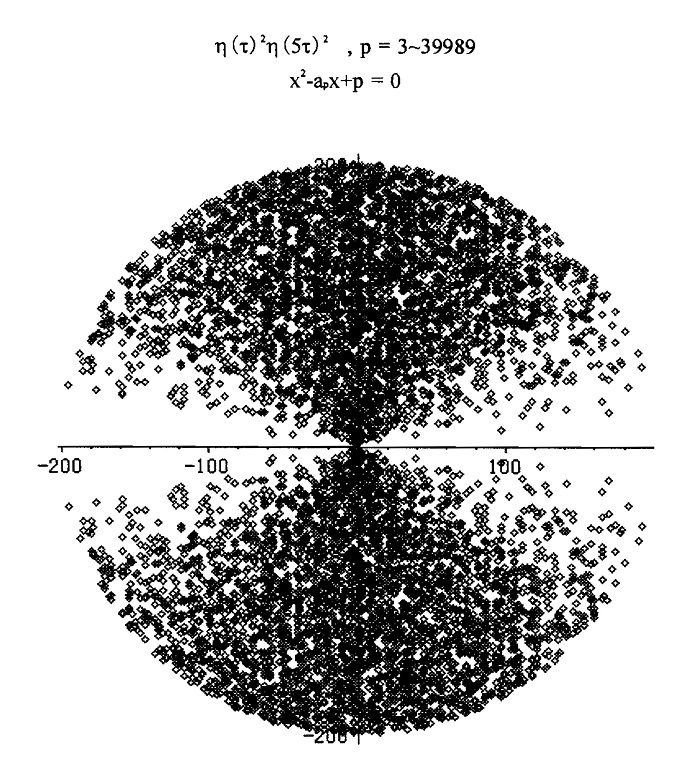
#数学 続き。添付図は http://www2.tsuda.ac.jp/suukeiken/math/suugakushi/sympo16/16_8nanba.pdf … より。複素根をすべてプロット。素数pが4万未満の場合のプロットなので、半径200の円内に入っていることがリーマン予想に類似のハッセの定理の特別な場合。pic.twitter.com/b7iAhf9Hkc

#数学 続き。偏角θで見た分布は(sin θ)^2分布になっていそうな感じ(佐藤・テイト予想が成立している感じ)も根のプロット結果を見ればわかります。 pic.twitter.com/b7iAhf9Hkc
#数楽 もう一度訂正。https://twitter.com/genkuroki/status/670988044418211840 …「類対論」ではなく「類体論」です。類体論入門の話は「平方剰余の相互法則」の話からするのが定番です。リンク先では素数p分の1の小数展開の(p-1)/2+1桁目を題材として扱うことによって〜続く
@genkuroki #数楽 続き〜、算数レベルの話の一部分として、平方剰余の相互法則の帰結の1つを説明しました。フレンケルさんも説明していた「素数位数の有限体での方程式の解の個数」を使った直接的説明の方がわかりやすいかも。やるべき計算は以下の通り。続く
@genkuroki #数楽 続き。以下、p,qは互いに異なる素数とします。(1)まず、素数pを固定して、2次方程式x^2=qの有限体F_pでの解の個数をたくさんのqについて計算します。解の個数はqをpで割った余りで決まることがわかります。これは当たり前です。なぜならば〜続く
@genkuroki #数楽 続き〜、有限体F_pで解を探すことは、方程式の両辺をpで割った余りが等しくなるような整数xを探すことと同じことどからです。x^2=qの有限体F_pでの解の個数はqをpで割った余りで決まることは当たり前。面白いのはここから。続く
@genkuroki #数楽 続き。p,qは互いに異なる奇素数であるとします。(2) 次にqの方を固定して、x^2=qの有限体F_pでの解の個数をたくさんのpについて計算してみて下さい。すると不思議なことにpをqで割った余りで解の個数が決まっていそうなことがわかります。続く
@genkuroki #数楽(3)x^2=qの有限体F_pでの解の個数N(p,q)の表を作ると、p-1またはq-1が4で割り切れればN(p,q)=N(q,p)が、どちらも4で割り切れないならN(p,q)≠N(q,p)が成立していそうなことがわかる。これが平方剰余の相互法則です!
@genkuroki #数楽 これは実際に計算してみると、不思議な気分になります。実際に計算してみると何度でもびっくりできる。実は証明をいくつか知っていても不思議な気分が残ります。数学的に面白い結果では、証明を知っていても不思議な気分が残ることが多い。
#数楽 続き。整数aを固定して、二次方程式x^2=aの素数位数pの有限体F_pでの解の個数N_pの表を作ると、pが2aの約数でないとき、N_pはpを4aで割った余りだけで決定されることを確認できます(平方剰余の相互法則の帰結、そのときN_pは0または2)。続く
#数楽 続き。たとえば、11以上の素数pについてx^2=10の有限体F_pでの解の個数を求めることは、1/pの10進小数展開の((p-1)/2+1)桁目が0か9かを見ることと同じになります。これがリンク先の話のもとネタです→ https://twitter.com/genkuroki/status/670988044418211840 …続く
#数楽 続き。乗法群F_p^×は位数p-1の巡回群になるので、10の平方根がF_pの中に存在するための必要十分条件は10^{(p-1)/2}をpで割った余りが1になること、すなわち10^{(p-1)/2+1}をpで割った余りが10になることだと分かります。続く
#数楽 続き。一つ前のツイートに書いた内容が理解できなくても、10,100,1000,…をpで割った余りを計算することであれば小学生でもできます。その計算は実質的に1/pを小学生のときに習う筆算で小数展開する計算と完全に同じになります。続く
#数楽 続き。たとえば、(i)1/13の小数展開を割算の筆算で計算してみる。(ii)1,10,100,1000,…を13で割った余りを計算してみる。(iii)1,10,100,1000,…を13で割った余りがそのまま1/13の筆算による計算の中にそのまま出て来ることを確認できる。
#数楽 続き。1/13の筆算に出て来る余りは順番に1,10,9,12,3,4,1,10,…です。1,10,9,12,3,4が「循環節」です。長さは6=(p-1)/2です。10^rを13で割った余りが1になるとき、10^{r+1}}を13で割った余りは10になります。続く
#数楽 続き。一般にpが11以上の素数のとき、1/pの小数展開の筆算による計算をr桁目までしたときの余りで1が出て来ることと、10^rをpで割った余りが1になることは同値であり、その次のr+1桁目は10をpで割った商と余りの商になるので0になります。続く
#数楽 続き。p=11,13,17,…に対する1/pの循環節が分かるところまで計算すれば、筆算の途中で余り1が出て来たら、その次の桁が0になることは明らかであることがわかるはずです。こういうことは実際に計算してみた人だけがわかる。続く
#数楽 素数p=11,13,17,…について1/pの小数展開を大量に計算して行けば,p-1桁目まで計算したところで必ず余り1が出て来てその次の桁0になることを確認できます。1/pの第(p-1)+1桁目は必ず0になります。面白いのはその半分の(p-1)/2+1桁目です。続く
#数楽 続き。素数p=11,13,17,…について1/pを小数展開すると、(p-1)/2+1桁目は必ず0または9になります。しかも半々でそうなっていることがわかります。その0と9のどちらになるかがpを40で割った余りだけで決まることが平方剰余相互法則の帰結の一つ。続く

#数楽 続き。【資料1】添付画像は120未満の素数p分に対する1/pの小数展開の表。pが11以上のとき、(p-1)/2+1桁目が0または9になっていることを確認できる。pic.twitter.com/paFXqcMb9q
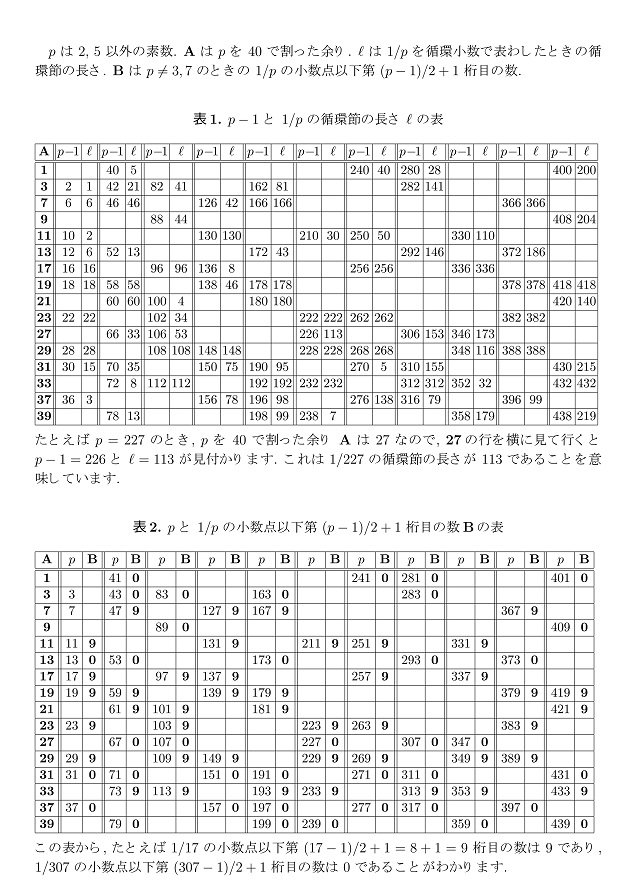
#数楽 続き。【資料2】添付画像は素数pを40で割った余りで分類して1/pの小数展開に関するデータを整理し直したものです。循環節の長さが(p-1)/2の約数になるか否かがpを40で割った余りで決まっていることがわかります。pic.twitter.com/P4DBUXWnWg
#数楽 続き。「素数pに対する1/pの循環節の長さが(p-1)/2の約数になるか否かがpを40で割った余りで決まっている」という事実は算数で出会うことができる真に不思議な数学的結果です。しかも、循環小数の循環節を求める計算は算数好きな小学生なら必ずやっている。続く
#数楽 続き。その結果は「pが2と5以外の素数のとき、2次方程式x^2=10の有限体F_pでの解の個数はpを40で割った余りで決まっている」と言い変えられます。この結果を使うと無限にある素数pに対する有限体F_pでの解の個数を有限的な計算で求めることができる!続く
#数楽 続き。平方剰余の相互法則(類体論の最も簡単な場合)を使えば、無限個の素数pに対する方程式x^2=aの有限体F_pでの解の個数が有限的な計算で全部わかってしまう。これと類似の問題を(2変数x,yの3次式)=0の形の方程式で考えたものが谷山・志村・ヴェイユ予想です。続く
#数楽 続き。その話題での「いつもの例」は「方程式y^2+y=x^3-x^2の有限体F_pでの解の個数はq(1-q)^2(1-q^{11})^2(1-q^2)^2(1-q^{22})^2…の展開のq^pの係数a_pによってp-a_pと表される」という結果です。続く
#数楽 「与えられた方程式の無数にある素数位数pの有限体F_pでの解の個数のことがよくわかる」という話をしたのですが、「よくわかる」の意味合いを変えることによって別の予想・定理の話をすることもできます。続く
#数楽 方程式x^2=aの有限体F_pでの解の個数はpが2aの約数でなければ0または2になります。そして0と2がちょうど半々で出て来ます。たとえば方程式y^2+y=x^3-x^2の場合にも解の個数の分布の仕方が分かるというのが佐藤・テイト予想です。
#数楽 佐藤・テイト予想以前の話として、y^2+y=x^3-x^2の場合にはリーマン予想の類似の結果(ハッセの定理)も述べることができて、「y^2+y=x^3-x^2の有限体F_pでの解の個数とpの差は2√p以下になる」というのがハッセの定理の特別な場合です。続く
#数楽 ハッセの定理によってy^2+y=x^3-x^2の有限体F_pでの解の個数N_pはp±2√pのあいだに分布するのですが、N_p=p-2√p cos θ_pで0≦θ_p≦πを定めるとき、θ_pたちの分布がsin^2 θ dθ型になるというのが佐藤・テイト予想の特別な場合。
#数楽 で、その(sin θ)^2 dθ分布はSU(2)の固有値の組(e^{iθ},e^{-iθ})の分布だと解釈される。ジーナスnの場合にはUSp(2n)の固有値の分布を見れば良いらしいです(ジーナス2以上の場合の佐藤・テイト予想の類似はまだ証明されていない(はず))。
@genkuroki #数楽https://twitter.com/genkuroki/status/675147297563541510 …数セミ2016年2月号(2016年1月12日発売)の特集がちょうど「平方剰余の相互法則」のようですね。http://www.nippyo.co.jp/magazine/7010.html …
#数楽 おお、これは楽しい。「ゆっくり、のんびり」ではなくすぐに答えを見たければ、SHIFT+緑旗クリックでターボモードに。>Scratch(プログラム言語)で佐藤・テイト予想(sin^2θ予想)を確認。 #数楽 http://bit.ly/1NwotWf
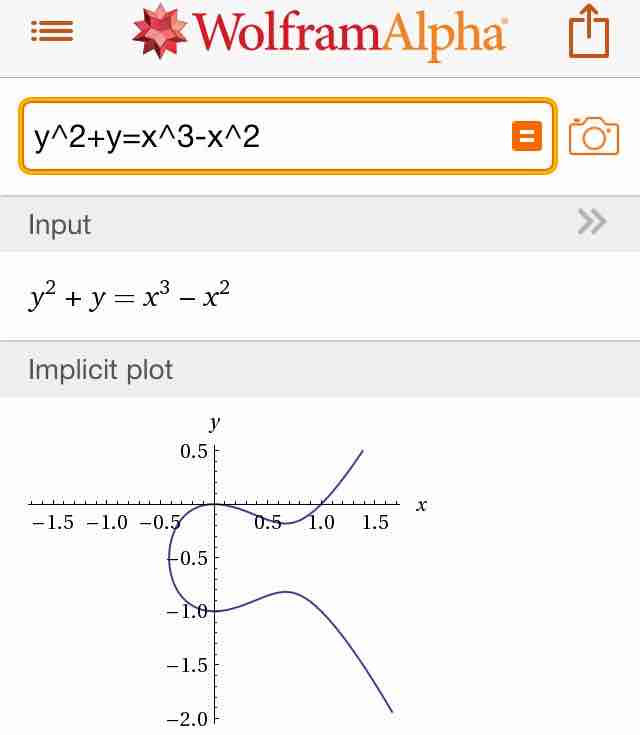
@genkuroki #数楽 添付画像はx,yに関する3次方程式y^2+y=x^3-x^2で定義される楕円曲線を実平面でプロットしたものです。方程式の解を実数の範囲内で求めてグラフを描いたものです。pic.twitter.com/G6GxYABecU
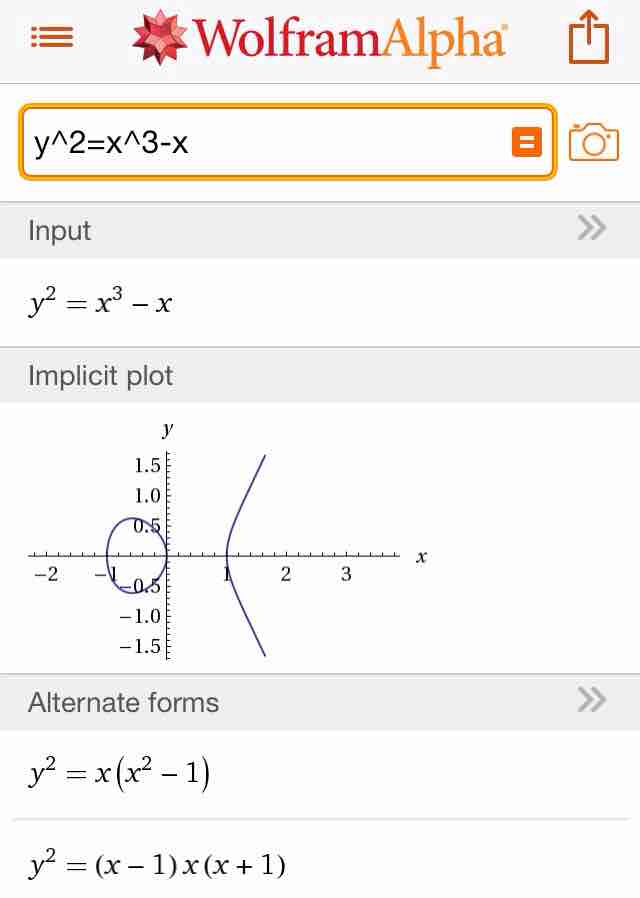
@genkuroki #数楽 添付画像は別の楕円曲線y^2=x^3-xの実平面でのグラフです。こういうときにWolframAlphaはとても便利です。pic.twitter.com/J2HuymOpvw
@genkuroki #数楽 楕円曲線の数学に関して大事なことの一つはx,yに関する3次方程式の解を探す範囲を実数に制限する必要がないことです。例えば複素数や有限体の中に解を探してもよい。複素数の中で解を探すと、楕円曲線は巨大なトーラス状の実曲面になっていることがわかります。

@genkuroki #数楽 pic.twitter.com/J2HuymOpvw添付画像は実数の範囲内で楕円曲線をプロットしたものです。複素数まで範囲を広げると巨大なトーラス状の曲面になっているのですが、その実平面による断面が見えていることがわかります。

@genkuroki #数楽 pic.twitter.com/J2HuymOpvwグラフの卵型の部分はトーラスを切って出る輪っかの一つです。右側の広がっている部分も実は無限遠(射影平面上で考える)で上下が繋がっていて輪っかになっています。トーラスの断面(輪っかが2つ)が見えている。
@genkuroki #数楽 実平面による切断面を眺めるだけではなかなか納得できないことですが、複素数の扱いを学ぶと、楕円曲線を定義するx,yに関する3次方程式を複素数の範囲内で解いて「プロット」して無限遠点を付け加えるとトーラスになることがわかります。
#数楽 http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160501StirlingFormula.pdf … Ver.0.14(50頁)。確率分布の解説にギャンブルに関する逆正弦則、ウィーグナーの半円則、佐藤・Tate予想に現われるsin^2分布に関する超簡単なコメントを追加。他にも色々追加してついに50頁になった。
#数楽 原点を中心とするn次元球面上の一様分布のx_1軸への射影について。まず、公平なギャンブルにおける浮いている時間の割合に関する逆正弦法則に登場する逆正弦分布は、1次元球面=円周上の一様分布の射影になっています。0〜1に台を持つ確率密度はdx/√(x(1-x)). 続く
#数楽 続き。ベータ分布の特別な場合であり、二項分布のベイズ推定でのJeffreys事前分布として試しに使ってみた人は結構いるはず。その分布は(1/2,0)を中心とする半径1/2の円周上の一様分布のx軸上への射影に一致しています。この一致にどれだけの意味があるのか?続く
#数楽 4次元空間{(x,y,z,w)}内の原点を中心とする3次元(表面が3次元)の単位球面x^2+y^2+z^2+w^2=1上の一様分布のx軸上への射影の確率密度は-1から1に台を持ち、(π/2)√(1-x^2))dxになります。続く
#数楽 続き。スケール変換と平行移動でその分布はBeta(3/2,3/2)分布に移る。一般に表面がn次元の原点を中心とする球面上の一様分布の原点を通る直線上への射影の同様な変換はBeta(n/2,n/2)分布になります。n=2の普通の球面だと一様分布になってしまう。続く
#数楽 続き。で、4次元空間内の3次元球面の直線上への射影で出て来る本質的にBeta(3/2,3/2)分布は21世紀の数論における最も深い結果の一つに出て来ます。その深い結果とは佐藤・Tate予想の解決!詳しくは→ http://twilog.org/genkuroki/search?word=佐藤 sin 予想&ao=a …
#数楽 続き。佐藤・Tate予想の解説によく出て来る楕円曲線 y^2+y=x^3-x^2 のケースであれば、コンピュータに強ければ数値的に分布を自分で確認できます。その方法の解説は https://twitter.com/genkuroki/status/671257536218193920 … にあります。続く
#数楽 続き。なぜか、楕円曲線の素数位数pの有限体上での点の個数を数えてその適切なスケール変換の結果の素数pを動かしたときの分布を見ると、なんと3次元球面上の一様分布の射影に一致していることがわかるという不思議な話です。
#数楽 続き。数論における最も重要な数学的対象はゼータ函数とその仲間たちです。ゼータ函数は素数に関わる「統計」の母函数だとみなせます。統計科学の素養のある人が数論も楽しめるということはあっても不思議ではないことだと思われます。私の興味はそれとは逆向きなのですが。
#数楽 ワイルズさんがフェルマー予想を解決したことは有名だと思います。佐藤・Tate予想の解決はその方向でのさらに深い結果です。佐藤幹夫さんがどのようにして真の分布の推定に成功したかに関しては http://www2.tsuda.ac.jp/suukeiken/math/suugakushi/sympo16/16_8nanba.pdf … に書いてあり、とても面白いです。
#数楽 (p_1,…,p_r)が確率分布であるとはp_i≧0かつΣp_i=1をみたすことでした。そのような(p_1,…,p_r)全体のなす図形は「r-1次元単体」と呼ばれています。0次元単体は1点。1次元単体は線分。2次元単体は正三角形。3次元単体は正四面体です。
#数楽 佐藤・Tate予想に出て来る3次元球面上の一様分布の正体はリー群SU(2)上のハール測度。そして直線上への射影は共役類の空間への射影(本質的に2×2行列のトレースを取る操作)に対応しています。SU(2)では共役類←→特性多項式。特性多項式が楕円曲線のゼータに対応。
#数楽 "(2/2) ラングランズ・プログラム、谷山・志村・ヴェイユ予想、佐藤・テイト予想"https://twitter.com/i/moments/844841644524392448 …



